Cellular Automata, in Excel

This post is about cellular automata, a topic in discrete math. I made an implementation of "Conway's Game of Life" in an Excel spreadsheet.

Conway's Game of Life is described as follows (from Wikipedia):

The universe of the Game of Life is an infinite two-dimensional orthogonal grid of square cells, each of which is in one of two possible states, alive or dead. Every cell interacts with its eight neighbours, which are the cells that are horizontally, vertically, or diagonally adjacent. At each step in time, the following transitions occur:

1. Any live cell with fewer than two live neighbours dies, as if caused by under-population.
2. Any live cell with two or three live neighbours lives on to the next generation.
3. Any live cell with more than three live neighbours dies, as if by overcrowding.
4. Any dead cell with exactly three live neighbours becomes a live cell, as if by reproduction.

The initial pattern constitutes the seed of the system. The first generation is created by applying the above rules simultaneously to every cell in the seed—births and deaths occur simultaneously, and the discrete moment at which this happens is sometimes called a tick (in other words, each generation is a pure function of the preceding one). The rules continue to be applied repeatedly to create further generations.

Basically, someone sets up an initial pattern (the "seed") and then it develops on its own following the rules listed above. Patterns can remain static, repeat periodically, run for a while then die out, or continue indefinitely. Conway's Game of Life is well-known as an instance of very complex behaviour emerging from simple rules and interactions.

To implement it in Excel, I took the following steps:

1. I made a grid for the initial seed values; each cell would be either 0 or 1 to indicate dead or alive, respectively.
2. I made a grid, of the same size, for the first step after the initial seed that looked at the corresponding cell from the previous grid, along with its eight neighbours to determine what its new state should be. Here is the Excel function I used: =IF(C3=1,IF(SUM(B2:D4)<3,0,IF(SUM(B2:D4)>4,0,1)),IF(SUM(B2:D4)=3,1,0))
3. I left empty space around the edges of each iteration's grid to provide a boundary condition of dead (i.e. 0) cells.
4. The grid from step 2 was copied-and-pasted repeatedly, using relative referencing so that it always looked at the previous iteration, not just the initial seed.
5. I applied conditional formatting (discussed here) to each iteration step to colour live cells black and dead cells white.

Once that was done, a pattern could be entered into the initial grid and its development over time could be seen by scrolling past the subsequent grids. To capture things better, I made a .gif (the internet's favourite image format!) that stitched together screenshots of each iteration:

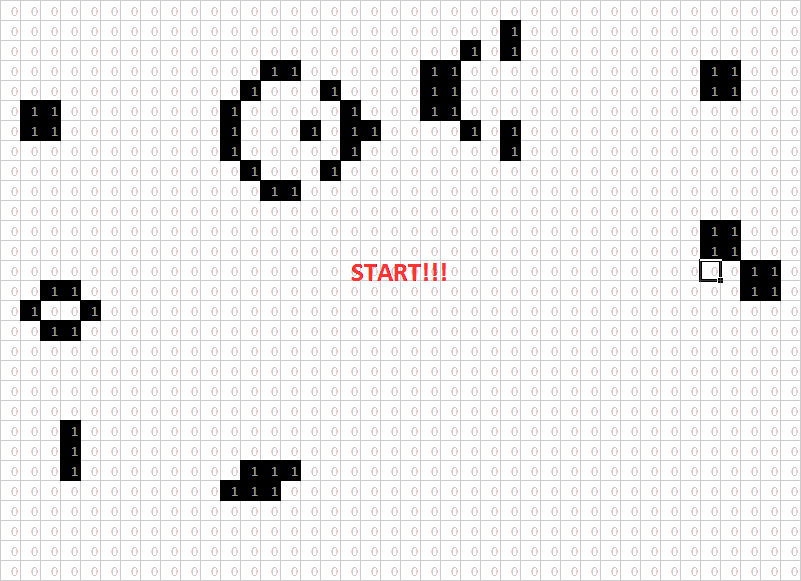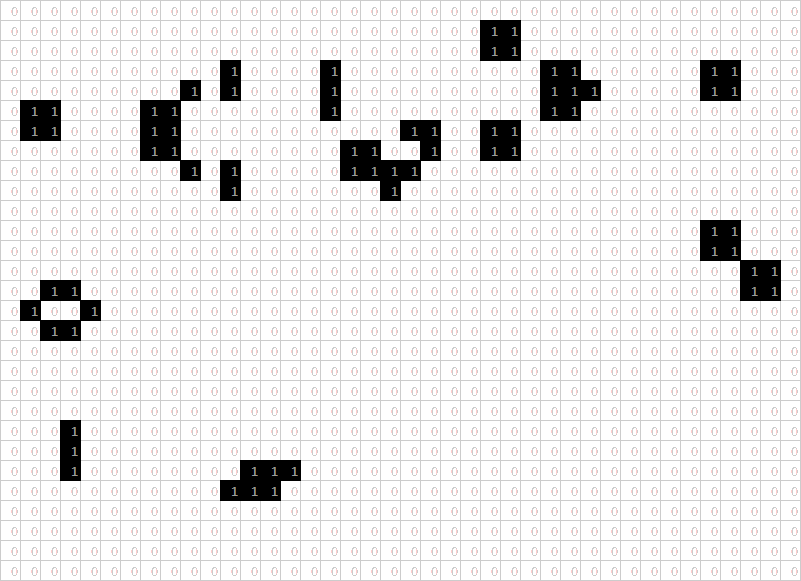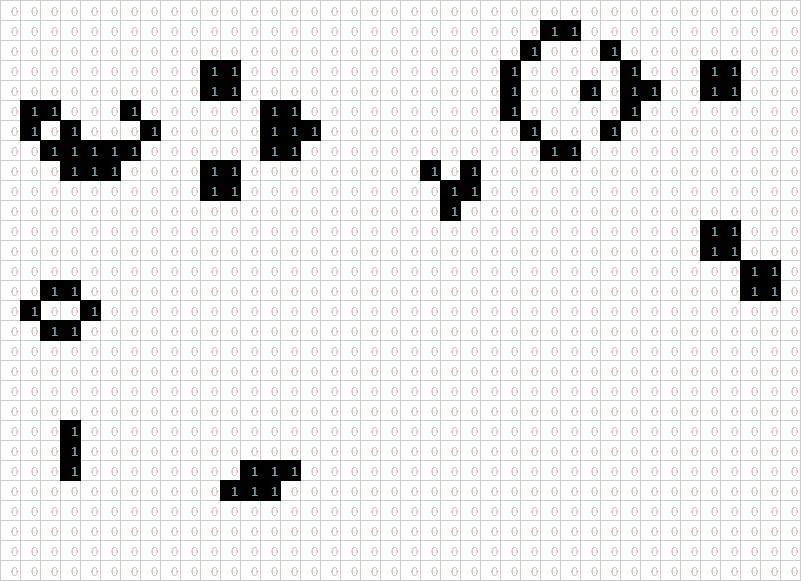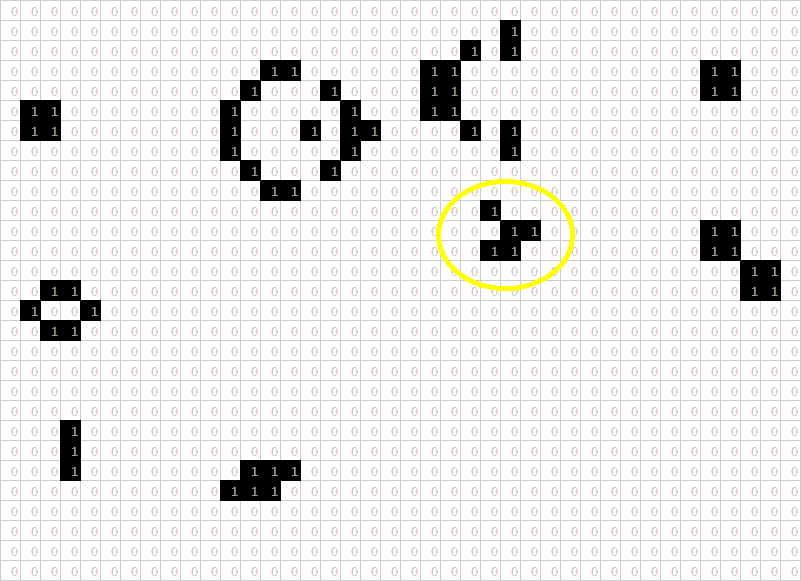
This sequence of screenshots represents 31 iterations of a "glider gun" pattern, along with some static and oscillating objects along the edges. At the end of the .gif, there is a group of live cells (circled in yellow) that weren't there to begin with, while all of the original live cells have persisted—this pattern will continue indefinitely and keep growing in population. Continuing to run the pattern would generate more gliders.

As an aside, I made the .gif in GIMP, following these instructions. Each frame (i.e. a screenshot of one iteration) was dragged-and-dropped into GIMP; they were automatically pasted as separate layers, which became frames when it was saved as a .gif. The linked instruction describe optimizing the animation and converting to indexed colours.

More About Cellular Automata

An interesting topic in Conway's Game of Life is the different speeds at which patterns can propagate across the grid.

Each cell in Conway's Game of Life can be represented as a Finite-State Machine:

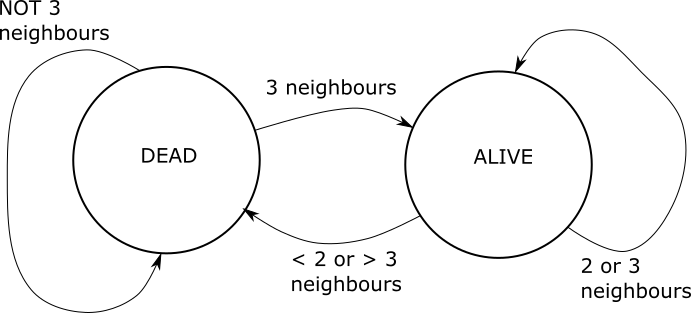
The mathematician Stephen Wolfram has done a lot of work on cellular automata.

As an example of the achievable complexity, some people have implemented logic gates (and even simple computers) in Conway's Game of Life. The following video by Alex Bellos provides a demonstration.

Finally, it gets tedious to really increase the number of iterations or the size of the grid that can be used in an Excel implementation, so anyone that wants to play around with different seed patterns can try this interactive online implementation.

If you liked this post, check out a previous one, where I did something similar with a fractal in Excel.

Permalink