DIY Telescope Project
This post is about a project I have planned for the next several months (or longer), to try to build my own telescope. I'll try to write a follow-up post to share how it turns out. My goal is not to build a high-quality telescope, but rather one that can be easily assembled from cheap and easy-to-find components.
The type of telescope I plan to make is a "Dobsonian", which uses a Newtonian optical arrangement and a altitude-azimuth mount. I found a tutorial here, although I don't intend to follow it too closely.
Components
Here are the components of the telescope, and the materials I'll be using (where I've decided so far):
- Primary mirror = a concave/magnifying bathroom mirror (i.e. for shaving and applying makeup); getting an off-the-shelf primary mirror was key to my objective of keeping it cheap
- Tube = a concrete sonotube (150 mm diameter), painted flat black
- Diagonal = a small mirror mounted on a 3d-printed bracket (see below for the design)
- Eyepiece = a 40 mm diameter ABS pipe, with a small off-the-shelf magnifying glass attached
- Mount = constructed of pine boards, with a lazy Susan bearing
- Plus miscellaneous hardware
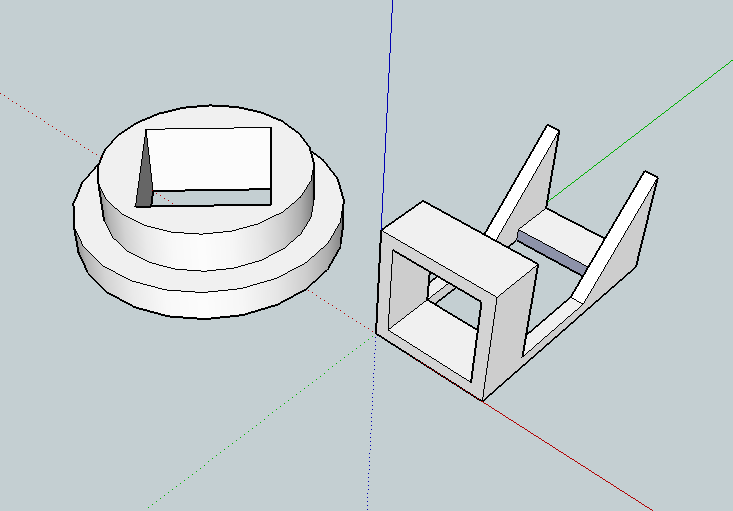
(At the moment, my 3D Printer is in need of a new hot end).
Design

Along with online resources, I cracked open my physics textbook to refresh my memory on optics equations. Here are some of the relevant equations and principles:
- The focal length, f, of a concave mirror equals half of its radius of curvature, r (i.e.
f = 0.5r) - The distances from the mirror to the object (p) and the image (i) are related to the focal length as follows:
(1/p) + (1/i) = (1/f) - The magnification, m, is
m = i/p - Stars are very far away, of course, and as p → ∞, i ≈ f
- The focal ratio (often presented in f-number notation) is defined as the focal length divided by the aperture
- A large aperture allows the telescope to collect more light
- The total distance (through diagonal) from the objective mirror to the eyepiece lens is the sum of their focal lengths
See here and here for a couple of ray diagrams of Newtonian optical assemblies for telescopes. Wolfram Alpha's demonstration site has an interactive calculator for Newtonian telescopes.

I measured my mirror's diameter at 167 mm and the depth at the centre to be 2.5 mm. This gives it a radius of curvature of 1400 mm and thus a focal length of 700. The aperture is the smaller of the mirror diameter and tube diameter, which is 150 mm. This gives it a focal ratio of f/4.67.
Another way to check the focal length is to find the point where the image in the mirror disappears as it transitions from upright to inverted; when the object distance (p in the formula above) equals the focal length (f), the image distance (i) becomes undefined.
Construction and Application
I might take advantage of the Fredericton Makerspace to do some of the work on this project.
When (if) I get it finished, I'll try to share some photos of the telescope (with labels and showing some of the assembly details, hopefully), along with any images I can capture through it.
There are some "dark sky preserves" in New Brunswick at Mt. Carleton Provincial Park and Kouchibouguac National Park. They'd be fun spots to take the telescope once it's completed.