(Rocket)ship in a bottle

It's hard to believe we're already a month into 2020. This post looks back at something I built as a Christmas gift for some kids.

Bottle rockets are a fun toy. Unlike most rockets, they don't rely on combustion. This makes them safer to play with, and also means that the materials used don't need to stand up to high heat, just moisture and moderate pressures—used pop bottles work great. The conventional style uses water and compressed air (although there are other combinations like pop + butane). The compressed air provides the energy and the water gives it something to push against. Recall that Newton's Third Law states that every action has an equal an opposite reaction: all rockets need something for a "reaction mass" (although if combustion is involved it is usually just the exhaust gases rather than adding an extra substance).

Like I said in the introduction, I built a bottle rocket launcher as a Christmas gift. Here's a picture of it in action:  

Here's a look at the launcher and its components. It comprises a support board, a platform with a circular hole to support the bottle, an air pump (intended for bike tires), and some tubing and fittings to connect the pump to the bottle.

Here's a close-up of the tubing and fittings. There is a rubber stopper (53/64" to 63/64" I.D.) that fits into the mouth of a pop bottle; an inflation needle was pushed through it to allow air to get into the bottle. 5/16" tubing connects the needle to the air pump via a quick-connect fitting (so that the water in the bottle won't leak out while the air pump is being hooked up).

To launch a bottle rocket, you fill a bottle part-way with water (see the discussion below for how much), insert the stopper (as tight as possible), invert the bottle and place it in the hole on the launch pad with the tube hanging loose, join the tube to the air pump with the quick-connect fittings, and pump until the stopper pops off and the rocket launches.

The book The Secret Life of Equations by Rich Cochrane (previously mentioned here) has an entry on the Tsiolkovsky Rocket Equation. It explains that,

The rocket equation tells us how much acceleration we can generate given the weight of the rocket, the weight of the fuel and the efficiency of the engine. In particular, it says that adding more fuel gives only a logarithmic increase in acceleration, which means that building rockets that can hold more and more fuel giver ever-diminishing returns.

Here is the rocket equation, along with a couple of other ones (Bernoulli's equation and the work to compress air, W = P dV (which equates to the energy stored in compressed air), both rearranged to convenient forms with nil variables cancelled out) that are relevant to bottle rockets:

Δv = v_ex ln (m_i/m_f)

v_ex² = 2 ((P₂ – P₁)/ρ_w)

W = P₂ V₂ ln (P₁/P₂)

In these equations, v is for velocity, m is for mass, V is for volume, and P is for pressure (absolute, not gauge). The subscript 2 indicates conditions inside the bottle while 1 indicates outside (i.e. atmospheric). "Delta v" is the maximum change in velocity (which is the speed it could reach starting from zero) of the rocket in the absence of other forces; in reality it will be slowed down by gravity and air resistance. The exhaust velocity in the rocket is calculated from the second equation using the difference in the pressure within and outside the bottle. The final mass of the rocket is that of the empty pop bottle used while the initial mass mainly consists of the amount of water added. In the third equation, it can be seen that the energy stored is proportional to the pressure and volume of stored air.

I put these equations (along with some basic equations of motion) into a spreadsheet to make a model to estimate how high a bottle rocket could be fired. It has some simplifications (e.g. the jet of water is assumed to be exhausted from the bottle at a constant velocity based on the initial difference in pressure, rather than decreasing as the compressed air expands as the water leaves, although it is restricted to not have a kinetic energy higher than the energy that was stored in the compressed air) but at least puts a boundary on the heights that could be achieved. Here's a graph from this model (the x-axis is how much water is added to a 1 L bottle):

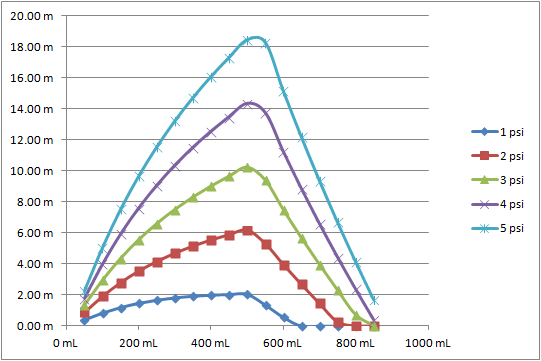
Even if it's just an approximation, the model (and examining the equations) makes some practical suggestions for launching bottle rockets:

• You need to leave room for both water (reaction mass) and air (energy) in your bottle. Too little water and the mass ratio in the rocket equation won't be sufficient; too much, and the volume available for compressed air won't provide enough energy. In the model, half full appeared to be the right balance, but in practice it seemed closer to a third full.
• A bigger bottle (e.g. 2 L vs 500 mL) is better, as it can have more volume for air and a higher mass ratio at the same time.
• A higher pressure has a big impact. In practical terms, using tape to get a better seal between the stopper and the bottle allowed for more air to be added before the bottle popped off, and thus greater heights to be reached.

The Christmas holidays also brought plenty of time to play board games with family and friends (and some new ones to try). I'll briefly mention a couple of highlights to wrap up this post:

Pandemic: Rising Tide has the theme of controlling flooding in the Netherlands, and the cooperative mechanics that the Pandemic series is known for: players compete against the game, which stochastically escalates in difficulty; either it spirals out of control and you lose, or you win together before that happens. Players need to balance urgent goals of repairing dikes and draining floodwaters with longer-term goals of building protective infrastructure.

Hive: Carbon is similar to chess in some ways. There are a small number of pieces (with multiples of some) and they each can move in a certain way. The goal is to surround your opponent's Queen (Bee). The most obvious difference from chess is that it is not played on a board. All of the pieces must always be touching; between that constraint and the geometry of the hexagonal tiles, the available positions are defined by the pieces themselves. Here's an example of a game:

For more of a strategic challenge, I'm wondering if different shapes of tiles could be included (e.g. squares + octagons or triangles + hexagons), such that the valid positions for a piece would be constrained further by where it will fit.

Permalink