Circles and Triangles
This post is about a book on geometry that I read last year (finishing up over the holidays).
Beautiful Geometry was written by Eli Maor and Eugen Jost. Each of its 51 chapters explains a topic in geometry and presents an artistic plate illustrating it. In addition to the artistic interpretations, there are plenty of diagrams to assist with the explanations. I found it to be well-written and effectively structured—the chapters tend to build on previous ones. The ancient Greeks considered geometry as the core of mathematics; in modern times it doesn't always get as much attention as other fields. Beautiful Geometry is a worthwhile read if you think geometry deserves some attention. I definitely learned some things from this book, and even with respect to material that I was familiar with, I still enjoyed the clear explanations and the illustrations.
In this review, I'm going to share some things from Beautiful Geometry that I found interesting.
The arithmetic mean is the familiar average (sum divided by n). The geometric mean is the n-th root of the product of n numbers and the harmonic mean is n divided by the sum of the reciprocals. One of the early chapters (chapter 10) had some theorems about these means.
A well-known theorem says that of the three means, the harmonic mean is always the smallest, the arithmetic mean is the largest, and the geometric mean somewhere in between.
The geometric mean of [numbers] is also the geometric mean of [their arithmetic mean and harmonic mean].
The book included geometric proofs for these theorems.
Theorems from Euclid (one of those ancient Greeks) feature prominently in the early chapters. Chapter 12 ties a couple of them together, concerning lines that cut a circle:
The two theorems we just met—numbers 35 and 36 in book III of Euclid—sound strikingly similar: both are about a circle, a point P, and a line through P the cuts the circle at points R and S. The two theorems state that the product PR ✗ PS remains constant for all possible lines through P. Yet there is a difference: in theorem 35 P is inside the circle while in theorem 36 it is outside. ...
And yet a closer inspection will show that the two theorems are one and the same after all. For when we say that a point P is given with respect to a circle, we imply only that the distance OP from P to the center of the circle O is given, and nothing else.
These two theorems are combined into a single statement (it's much easier to follow with the diagrams they include):
If through a point P a line is drawn that cuts a circle (O,r) at points R and S, the product PR ✗ PS is constant for all possible lines through P. If P is outside (O,r), this product is the square of the tanget from P to [the circle].
I think conic sections are a cool topic because of the way they tie together types of curves that seem very different at first. Chapter 29 includes this description:
Imagine slicing a cone—for illustration's sake think of it as an ice cream cone—with a swift stroke of a knife. If you slice it in a plane parallel to the cone's base, you get a circular cross section. Tilt the angle slightly, and you get an ellipse. Tilt the angle even more, and the ellipse becomes narrower, until it no longer closes on itself: it becomes a parabola. This happens when the cut is parallel to the side of the cone. Increase the angle yet again, and you get two disconnected curves, the two branches of a hyperbola (provided you regard the cone as a double cone joined at its apex).
I'm reminded of this passage from Quicksilver by Neal Stephenson (it involves the fictional character Daniel Waterhouse interacting with Sir Isaac Newton):
Stretch a line, and another intersecting it, and rotate the former about the latter and it will sweep out a cone. Now shove this cone through a plane and mark every point on the plane where the cone touches it. Commonly the result is an ellipse, but if the cone's slope is parallel to the plane it makes a parabola, and if it's parallel to the axis it makes a two-part curve called a hyperbola.
An interesting feature of all of these curves—the ellipse, the parabola, and the hyperbola—was that they were all generated by straight things, viz. two lines and a plane. An interesting feature of the hyperbola was that far away its legs came very close to being straight lines, but near the center there was dramatic curvature.
Greeks, e.g., Euclid, had done all of these things long ago [this book is set in the 18th Century] and discovered various more or less interesting properties of conic sections (as this family of curves was called) and of other geometric constructions such as circles and triangles. But they'd done so as an expression of pure thought, as a mathematician might compute the sum of two numbers. Every assertion that Euclid, et al., made concerning geometry was backed up by a chain of logical proofs that could be followed all the way back to a few axioms that were obviously true, e.g., "the shortest distance between two points is a straight line." The truths of geometry were necessary truths; the human mind could imagine a universe in which Daniel's name was David, or in which Ipswich had been built on the other side of the Orwell, but geometry and math had to be true, there was no conceivable universe in which 2+3 was equal to 2+2.
...
Comets passed freely through space, their trajectories shaped only by (still mysterious) interactions with the Sun. If they moved on conic sections, it was no accident. A comet following a precise hyperbolic trajectory through the aether was a completely different thing from Daniel's just happening to trace a hyperbolic course through the English countryside [London to Cambridge, via Ipswich]. If comets and planets moved along conic sections, it had to be some kind of necessary truth, an intrinsic feature of the universe. ...
... by asking for data on the interactions of the moon and sea, and of Jupiter and Saturn, Isaac was as much as saying that these were all of a piece, that everything attracted everything—that the influences on (say) Saturn of the Sun, of Jupiter, and of Titan ... were different only insofar as they came from different directions and had different magnitudes. Like the diverse goods piled up in some Amsterdam merchant's warehouse, they might have come from many places and have different values, but in the end all that mattered was how much gold they could fetch on the Damplatz. ... In the case of Cœlestial Dynamics, the gold—the universal medium of exchange, to which everything was reduced—was force. The force exerted on Saturn by the Sun was no different from that exerted by Titan. In the end, the two forces were added together to make a vector, a combined resultant force bearing no trace of its origins. (pp. 673 – 676)
Another kind of curve is a catenary. It is described in Chapter 33:
One of the outstanding problems that occupied the mathematical world in the years immediately following the invention of the calculus was to find the exact curve taken up by a chain of uniform thickness hanging freely under the force of gravity. To the eye, a hanging chain looks very much like a parabola, but the Dutch physicist Christiaan Huygens (1629–1695) disproved this when he was just 17 years old. The mystery was solved in 1691 by three of the leading mathematicians of the time, who worked on it independently—Huygens himself (now 62), Leibniz, and Johann Bernoulli. To everyone's surprise, the shape turned out to be the graph of the hyperbolic cosine, (exp(x) + exp(-x))/2, which henceforth became known as the catenary.
In addition to the catenary, some members of the Bernoulli family also studied the properties of another curve (that looks quite similar) called a cycloid. Some more complicated curves that are derived from the cycloid—epicycloids and hypocycloids—are discussed in Chapter 36.
Euler may well be the most famous mathematician in history. One of his lesser-known discoveries is the topic of Chapter 37. The Euler line connects the centroid, circumcenter, and orthocenter of a triangle:
In any triangle, the circumcenter (the center of the circumcircle), the centroid (the intersection of the three medians, so called because it is the center of gravity of the triangle), and the orthocenter (the intersection of the three altitudes), all lie on one line.
A really interesting topic that I hadn't heard of before reading Beautiful Geometry is geometric inversion. Here is the description (from Chapter 38):
Consider a circle with center at O and radius 1. Two points P and Q on the same ray through O are called inverses of each other with respect to the circle if ... OQ = 1/OP.
...
Since inversion maps points that are close to the center onto points far away from it, we expect that figures should be greatly distorted when subjected to inversion. Yet in spite of this, some figures do not change at all. Clearly, every ray through O is mapped on itself, and a circle with center at O and radius r becomes a circle with the same center and radius 1/r. More surprising is the fact that a circle through O is mapped onto a straight line not through O, and vice versa.
A practical application of this concept is the Peaucellier inverter which can convert rotational motion to linear motion.
I've mentioned previously on this blog that I like fractals. I wanted to give an example of one of the plates from Beautiful Geometry in this review; this presentation of the Koch snowflake seemed like a fitting choice:

The book has many other topics that I haven't touched on in this review. For example, Maor and Jost have a lot to say about the connections between geometry and number theory (primes, Fibonnaci numbers, irrational numbers, etc.).
The appendix contains a number of additional proofs, as well as instructions for how to draw a regular pentagon using only a compass and straight-edge. It's based on an intermediate step of constructing a right-angled triangle with side lengths of 1 and 0.5 to obtain the golden ratio (the length of the hypotenuse + the short side)—the golden ratio is the distance between opposite vertices of a pentagon with unit side lengths. I decided to try this construction myself:
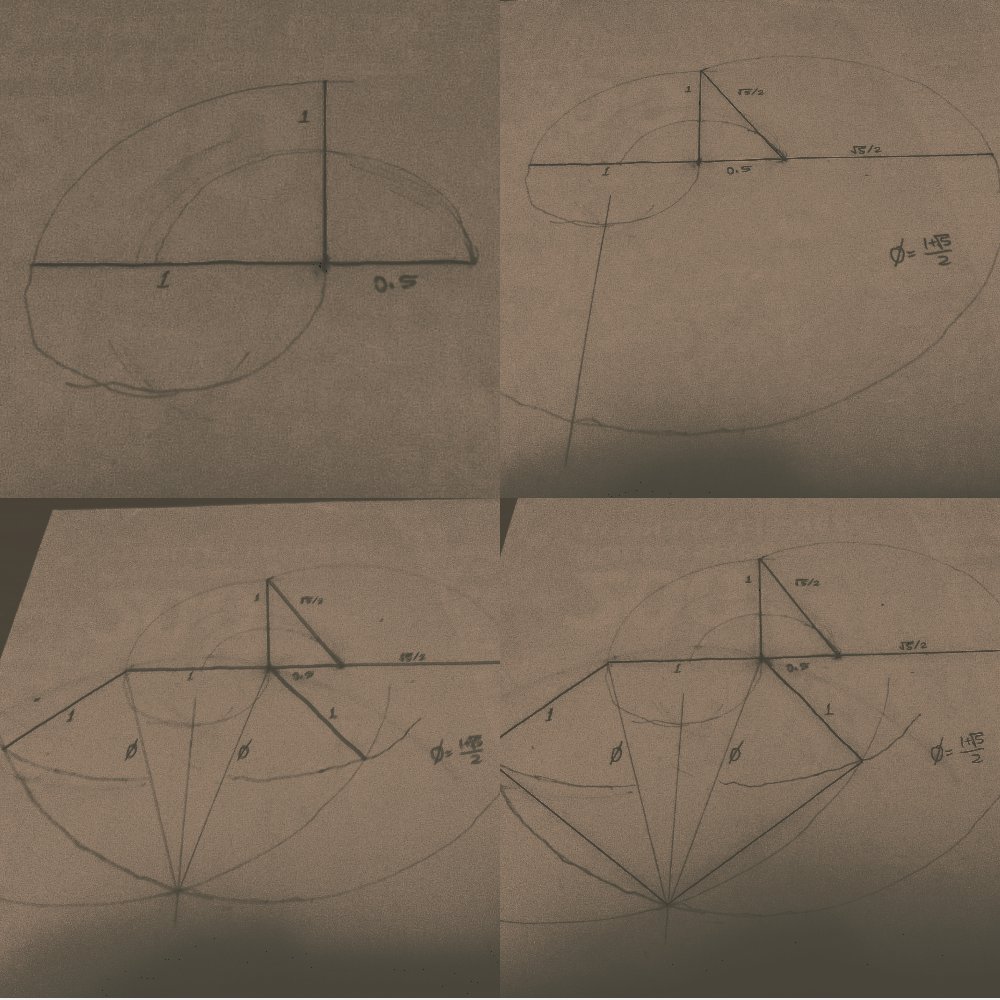
This figure shows the steps in the construction (left to right, top to bottom). It didn't turn out perfectly, probably due to not using a good quality compass (I just used a piece of string, which stretched and slipped a bit).
To finish this post off with a nod to its title, the 9 point circle is a circle that connects 9 significant points in a triangle.