Open Channel Hydraulics for Paddlers
This post combines two of my interests: engineering and paddling. During my undergrad studies (at the University of New Brunswick) I took a course called "Open Channel Hydraulics". Recently I decided to re-read some of my notes and textbooks and think about how they could provide insight for kayaking and canoeing on rivers. In addition to the practical applications, I hope it can illuminate some phenomena you might see while out on the water since I always find it's more satisfying when you understand what you're looking at.
To start with, what is an open channel? The "open" aspect refers to the fact that there is a free liquid surface exposed to the air, in contrast to flow in pipes (if they're full anyway). The "channel" aspect indicates that the water is semi-contained so that it only can flow in one direction; important geometric features of a channel are its slope in the direction of the flow and its cross-section (with a certain area and perimeter) perpendicular to the flow. For engineering purposes, there's a lot of attention paid to artificial channels (e.g. canals with a trapezoidal cross-section), but the equations and analytical tools are also relevant to natural channels (i.e. rivers). Because oceans (and large lakes) are not in a channel, this post isn't very relevant to sea kayaking.
The thematic thalweg of this post is the concept of energy—where it comes from and where it goes (since ultimately energy is conserved) in rivers. The following equation summarizes the three relevant components of energy in open channel hydraulics:
In this equation, z is the elevation (above sea level or another convenient datum), p is the water pressure, ρ is the density of water, g is gravity, and v is the velocity of the river. Each term has units of distance (metres in the metric system) so they can be compared on the same basis; their sum is known in engineering as the head—energy represented as the height to which water would rise in a standpipe. Because the pressure is zero at the surface and a maximum at the river bed, the second term (p / ρ g) equates to the water depth. The third term (v2/2 g) is the additional height from the surface that water would rise in a pitot tube (i.e. if its velocity was stagnated). The sum of the latter two terms (i.e. depth plus velocity head, ignoring elevation above sea level) is known as the specific energy.
As a river moves downhill/downstream, energy is moved between these three components and some is dissipated to the surroundings due to friction (this portion is known as headloss). The elevation, z, decreases along the water course; gravity feeds into the river's specific energy.
From the above equation, there are three sloping surfaces to consider:
- the river bed, at level z
- the water surface, at level z + (p / ρ g)
- the total energy, at level z + (p / ρ g) + (v2/2 g)
As a paddler, you can only consistently see surface 2 (although if the water is clear or shallow enough, you can see surface 1), but it is a good exercise to try to visualize the other surfaces. In slow-moving waters, surface 3 is almost touching surface 2, while the gap between them increases in fast currents. Surface 3 will always be sloped downstream as energy is lost (converted by friction to heat and noise) and its slope increases as the current does (because faster flows find more resistance from friction). So this means that surface 3 does not rise when the flow speeds up but rather surface 2 dips. Look at the flow around a rock and you can see this in action: in front of the rock the water mounds up a bit (surface 2 touching surface 3 at the point of stagnation) while at the sides the water surface dips (surface 2 separating from surface 3 as the velocity increases). When you add in the undulations of the river bed, you get slow-moving deep flow in pools (surface 2 is far from surface 1 and close to surface 3) and fast shallow flow in riffles (surface 2 is close to surface 1 and not as close to surface 3). Water can't flow up hill, but if surface 2 is far from surface 3 the gap between them can close quickly in a jump (discussed below), so having an intuition for these three sloped surfaces can help with your situational awareness on a river.
I'm trying not to get too heavily into hydraulic equations in this post, but one that is essential in open channel hydraulics is the Manning formula. The Fundamentals of Hydraulic Engineering Systems textbook by Hwang & Houghtalen explains that,
To solve open channel flow problems, we must seek the interdependent relationships between the slope of the channel bottom, the discharge, the water depth, and other given channel conditions.
The Manning formula ties these factors together:
As above, v is the velocity. The factor n relates to the channel roughness. It can't be measured in a practical way, but there are tables of suggested values depending on the conditions in the channel; most natural rivers would have n between 0.025 – 0.075. R is the "hydraulic radius", which is defined as the area of the flow's cross-section divided by the wet portion of the perimeter (so not including the top surface). For the purposes of this post, the average depth of the river is a decent enough approximation for R. S is the energy gradient, that is, the slope of surface 3 defined above. In a stretch of river with uniform, steady flow (i.e. constant depth and flow in space and time) the three slopes will be parallel, so it's probably more convenient to use the slope of the river bed in calculations since it can be practically measured.
We're looking at the Manning formula for what it can tell us about rivers, not to get out our calculators before going paddling, so I'm going to draw out some implications of the above equation. If everything else is held constant, increased roughness will decrease the flow velocity, increased depth (technically "hydraulic radius") will increase it (since more of the flow is away from the river bed where it is subject to friction), and increase slope will increase it. However, in reality it is usually flow that is fixed so the picture becomes more complicated. Flow is equal to the average velocity times the area of the cross-section. So if roughness decreases the flow velocity, a larger cross-section (i.e. increased depth) is needed to pass the same flow. Increasing the average depth will increase both the area and average velocity so the flow increases faster than the velocity alone (although once a river spills out onto its floodplain, the area of the cross-section can increase much more than the average depth does).
For an example of the Manning formula in action, I looked at the Nashwaak River between Durham Bridge and Penniac Island. The river drops around 5 metres over a distance of about 14,000 m (only around 12 km as the crow flies) for a slope of 0.00036. The flow reaches around 50 cubic metres per second after rainstorms in the summer and the width of the stream is around 60 metres. Assuming a roughness of 0.035 then an average depth of 1.3 m (4.3 ft) and a flow of 0.65 m/s (2.1 ft/s) satisfies the Manning equation.
Returning to the concept of specific energy introduced above, a fascinating implication is that, at a given flow, the same specific energy can occur at two different depths (with faster or slower velocities to arrive at the same flow). This is shown in the following graphs:
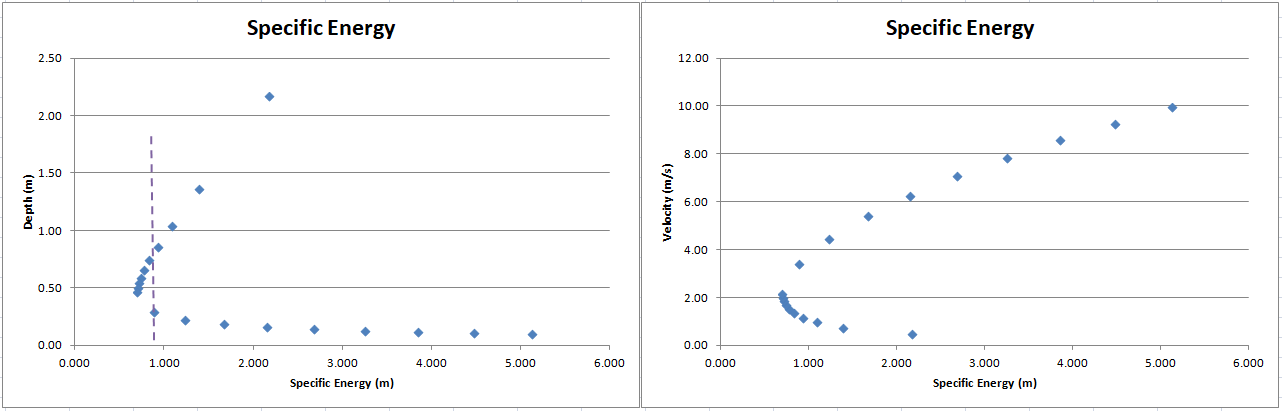
The chart on the left shows how a depth of 0.3 m can have the same specific energy as a depth of 0.75 m (at the flow I used in this example). The chart on the right has velocities; the higher branch of velocities goes with the lower branch of depths, and vice versa. In both graphs, it can be seen that the specific energy has a minimum value that is greater than zero—this is the minimum energy for conveying that flow. At this point, two-thirds of the specific energy is associated with the depth and one-third is associated with the velocity. The depth is known as the critical depth. When the water is deeper than the critical depth (the upper branch in the left graph and the lower branch in the right one) the flow is called "sub-critical" and when the water is below the critical depth it is called "super-critical" flow. If a barrier* is placed in a sub-critical stream that leaves less than the critical depth between the top of the barrier and the water surface than the water will pile up upstream until it can maintain the critical depth over the barrier. Downstream of a point where it passes through the critical depth, the flow will usually be super-critical.
*the barrier can be a natural feature like a seam of harder rock that doesn't erode as much as the stream bed leading up to it.
Super-critical flow is something paddlers should pay attention to, because it is where you can find features like standing waves and hydraulic jumps. In sub-critical flow, if you toss a stone into the water, the ripples will spread upstream and downstream. In super-critical flow, however, the current is faster than the speed that ripples move at so they can't spread upstream. Ripples from stationary features can end up with successive crests lining up in the same location. This forms a standing wave. A hydraulic jump—where the water level slopes upward going downstream—is possible because there is a higher depth with the same specific energy (also recall the discussion above about surface 3). I won't share the equation for hydraulic jumps here due to its complexity, but basically the more super-critical the flow is leading into the hydraulic jump, the higher of a jump is possible (Wikipedia has a useful table). Hydraulic jumps dissipate a lot of energy (so the analysis is more complicated than drawing a straight vertical line to find the alternate depth on a specific energy graph) so they should be treated with caution.
In the preceding paragraph, I mentioned that flow could be more super-critical. This notion is quantified by something called the Froude number. In hydraulics, there are several dimensionless numbers (the numerator and denominator have the same units) that compare the magnitude of the two dominant forces in a flow situation. The Froude number compares momentum and gravity, which are usually the most relevant forces in open channel situations (another such dimensionless number is the "Reynolds number" that compares momentum and viscosity). The Froude number, Fr, is defined as follows:
As in the previous equations, v represents velocity and g represents gravity. L in this equation is a characteristic length dimension, which will be depth in this application. A couple of things to note are that both the numerator and denominator have units of m/s (in the metric system) making the ratio dimensionless overall, and that the term in the denominator is the speed of a gravity wave (such as a ripple). For Froude numbers less than 1, the flow is sub-critical and for Froude numbers greater than 1, the flow is super-critical. In addition to the test of whether ripples can spread upstream (indicating Fr < 1), a more qualitative assessment comes from a memorable sentence in my course notes from UNB:
The bigger the Froude number, the louder the river.
The Froude number also has an application in the analysis of boat hulls and the wakes they form. In that case, the characteristic length used is the length at the waterline, rather than the water depth. This document from Tasmania has interesting diagrams showing how a boat's wake changes as the Froude number increases. If I understand correctly (this is a topic I'd like to learn more about), at a Froude number of 0.4, a boat starts climbing up its bow wave and it begins planing at higher speeds. So Fr = 0.4 is considered the "hull speed". In a 3.05 m (10 ft) kayak this works out to a speed of 2.2 m/s, while in a 4.88 m (16 ft) kayak (or canoe) this works out to a speed of 2.8 m/s. To repeat a quote from this book that I shared in this post,
Much of the power expended in propelling a ship goes into wave-making and anything that can be done to reduce these waves results in increased efficiency
Since a longer boat has the same kind of wake at a higher speed relative to a shorter one, it is able to move through the water more efficiently. This ties the discussion of hulls and wakes back into the energy-focused theme of this post. Waves carry energy, so wakes can be looked at as a type of wave that is carrying energy away from a boat.
Unlike for sea kayaking, waves are usually less of a consideration for paddling on rivers (only short period waves have a chance to develop) so I won't spend much time on waves in this post. The one notable aspect I'll mention is the difference between wave velocity and group velocity. Group velocity is the speed at which a packet of waves advances. It is only half of the velocity of an individual wave. The reason for this has to do with the leading edge of the group needing time to set up the oscillation where the next wave should be before the group can actually advance. Waves don't really carry water forward (unless they are breaking); they have a rotational motion in place and it's only the pattern that moves across distances. This discrepancy between wave velocity and group velocity is why, for example, it takes longer for the wake of a passing boat to reach you than it appears the wake is moving.
So far, I've discussed how hydraulic jumps and friction with the river bed can dissipate energy (and I've also mentioned how the power used to propel a boat goes into setting up its wake). The energy is not actually lost, but it gets converted to forms such as heat and sound that can't do anything more for how the river flows. Another type of feature in open channel flow that can dissipate energy is eddies. Eddies are circular turbulent disturbances. They start at the scale of the feature that created them, but spawn smaller eddies in an energy cascade down to a dimension known as the Kolmogorov microscale. This process was described in a ditty by Lewis Fry Richardson:
Big whorls have little whorls
Which feed on their velocity,
And little whorls have lesser whorls
And so on to viscosity.
When the water is calm I like drawing my paddle through it and watching the eddies that mark its passage.
One of the final things I want to discuss in this post is sediment. Rivers carry more than just water—they can carry significant amounts of clay, rock, and everything in between, depending on the flow and other factors. It is part of their dynamic nature that they carve their own channel (and can build deltas a significant distance out into the sea under the right conditions). The relevance of sediment to us as paddlers is in the clues it can provide about the possible flow velocities that can be experienced in a section of river. In general, a sand bar was probably deposited at a lower flow velocity than a gravel bar was, for example. The following chart (from Wikipedia) is not really in standard use anymore, but it still gives a general idea of the relationship between the flow velocity and the size of sand/rock grains that will be eroded or deposited or carried along:
This post has gotten long enough, so I'm going to wrap it up here, but there are certainly other topics that could be added to this exploration of how open channel hydraulics can apply to paddling. These include things like backwater and drawdown curves (gradually varied non-uniform flow), velocity profiles (across the width and depth of a cross-section), and flow nets as a visualization tool. I hope to do some more writing on this subject in the future. There are also some software programs for modelling/visualizing open channel flow and it might be neat to try to learn how to use some of them.